Sabtu, 06 September 2008

Matriks Balikan (Invers)

JIka A dan B matriks bujur sangkar sedemikian rupa sehingga A B = B A = I , maka B disebut balikan atau invers dari A dan dapat dituliskan B = A − 1 ( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan A = B − 1. Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.

Matriks A = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} dapat di-invers apabila ad - bc ≠ 0

Dengan Rumus =

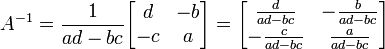
A^{-1} = \frac{1} {ad-bc}\begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix} = \begin{bmatrix} \frac{d} {ad-bc} & -\frac{b} {ad-bc} \\ -\frac{c} {ad-bc} & \frac{a} {ad-bc} \\ \end{bmatrix}

Apabila A dan B adalah matriks seordo dan memiliki balikan maka AB dapat di-invers dan (AB) − 1 = B − 1A − 1


Contoh 1:

Matriks

A = \begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix} dan B = \begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix}
AB = \begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix}\begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} = I (matriks identitas)
BA = \begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix}\begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} = I (matriks identitas)

Maka dapat dituliskan bahwa B = A − 1 (B Merupakan invers dari A)


Contoh 2:

Matriks

A = \begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix} dan B = \begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix}
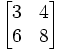
AB = \begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix}\begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix} = \begin{bmatrix} 3 & 4 \\ 6 & 8 \\ \end{bmatrix}
BA = \begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix}\begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix} = \begin{bmatrix} 17 & 21 \\ 15 & 19 \\ \end{bmatrix}

Karena AB ≠ BA ≠ I maka matriks A dan matriks B disebut matriks tunggal.


Contoh 3:

Matriks

A = \begin{bmatrix} 3 & 1 \\ 5 & 2 \\ \end{bmatrix}

Tentukan Nilai dari A-1

Jawab:

A^{-1} =\frac{1} {(3)(2)-(5)(1)}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \frac{1} {6-5}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \frac{1} {1}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix}


Contoh 4:

Matriks

A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \\ \end{bmatrix}, B = \begin{bmatrix} 3 & 2 \\ 2 & 2 \\ \end{bmatrix}, AB = \begin{bmatrix} 7 & 6 \\ 9 & 8 \\ \end{bmatrix}

Dengan menggunakan rumus, maka didapatkan

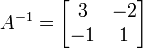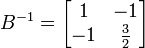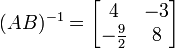
A^{-1} = \begin{bmatrix} 3 & -2 \\ -1 & 1 \\ \end{bmatrix}, B^{-1} = \begin{bmatrix} 1 & -1 \\ -1 & \frac{3} {2} \\ \end{bmatrix}, (AB)^{-1} = \begin{bmatrix} 4 & -3 \\ -\frac{9} {2} & 8 \\ \end{bmatrix}

Maka

B^{-1} A^{-1}= \begin{bmatrix} 1 & -1 \\ -1 & \frac{3} {2} \\ \end{bmatrix}\begin{bmatrix} 3 & -2 \\ -1 & 1 \\ \end{bmatrix} = \begin{bmatrix} 4 & -3 \\ -\frac{9} {2} & 8 \\ \end{bmatrix}

Ini membuktikan bahwa (AB) − 1 = B − 1A − 1

Diposting oleh di

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)