Komunitas SekolahRumah Pelangi Matematika: Interpolasi Polinomial

Dengan menganggap masalah pada interpolasi polinomial untuk deret n + 1 di titik (x₀,y₀)...., (x_n,y_n). Maka, kita diminta untuk menemukan kurva p(x) = a_m $x m$ + a_m-1 $x m - 1$ + ... + a₁x + a₀ dari sudut minimum yang melewati setiap dari titik data. Kurva ini harus memenuhi

$\begin{matrix} {y_0}& = &a_mx_0^m &+& a_{m-1}x_0^{m-1} &+...+& a_1x_0 &+& a_0\\ {y_1}& = &a_mx_1^m &+& a_{m-1}x_1^{m-1} &+...+& a_1x_1 &+& a_0\\ \vdots& &\vdots& &\vdots& &\vdots& &\vdots\\ {y_n}& = &a_mx_n^m &+& a_{m-1}x_n^{m-1} &+...+& a_1x_n &+& a_0\\ \end{matrix}$

karena x_i diketahui, ini akan menuju pada sistem matrik di bawah ini

$\begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^m\\ 1 & x_1 & x_1^2 & \cdots & x_1^m\\ \vdots & \vdots & \vdots & \cdots &\vdots\\ 1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^m\\ 1 & x_n & x_n^2 & \cdots & x_n^m\\ \end{bmatrix}$ $\begin{bmatrix} a_0\\ a_1\\ \vdots\\ a_{m-1}\\ a_m\\ \end{bmatrix}$ = $\begin{bmatrix} y_0\\ y_1\\ \vdots\\ y_{n-1}\\ y_n\\ \end{bmatrix}$

Ingat bahwa ini merupakan sistem persegi dimana n = m. Dengan menganggap n = m memberikan sistem di bawah ini untuk koefisien interpolasi polinomial p(x):

$\begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^n\\ 1 & x_1 & x_1^2 & \cdots & x_1^n\\ \vdots & \vdots & \vdots & \cdots &\vdots\\ 1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^n\\ 1 & x_n & x_n^2 & \cdots & x_n^n\\ \end{bmatrix}$ $\begin{bmatrix} a_0\\ a_1\\ \vdots\\ a_{n-1}\\ a_n\\ \end{bmatrix}$ = $\begin{bmatrix} y_0\\ y_1\\ \vdots\\ y_{n-1}\\ y_n\\ \end{bmatrix}$ (1)

Matrix di atas diketahui sebagai Matrix Vandermonde; kolom j merupakan elemen pangkat j-1. Sistem linier pada (1) disebut menjadi Sistem Vandermonde.

Contoh soal:

Cari interpolasi polinomial pada data (-1,0),(0,0),(1,0),(2,6) menggunakan Sistem Vandermonde.

Jawab:

Bentuk Sistem Vandermonde(1):

$\begin{bmatrix} 1 & x_0 & x_0^2 & x_0^3\\ 1 & x_1 & x_1^2 & x_1^3\\ 1 & x_2 & x_2^2 & x_2^3\\ 1 & x_3 & x_3^2 & x_3^3\\ \end{bmatrix}$ $\begin{bmatrix} a_0\\ a_1\\ a_2\\ a_3\\ \end{bmatrix}$ = $\begin{bmatrix} y_0\\ y_1\\ y_2\\ y_3\\ \end{bmatrix}$

Untuk data di atas, kita mempunyai

$\begin{bmatrix} 1 & -1 & 1 & -1\\ 1 & 0 & 0 & 0\\ 1 & 1 & 1 & 1\\ 1 & 2 & 4 & 8\\ \end{bmatrix}$ $\begin{bmatrix} a_0\\ a_1\\ a_2\\ a_3\\ \end{bmatrix}$ = $\begin{bmatrix} 0\\ 0\\ 0\\ 6\\ \end{bmatrix}$

$\begin{bmatrix} 1 & -1 & 1 & -1 & 0\\ 1 & 0 & 0 & 0 & 0\\ 1 & 1 & 1 & 1 & 0\\ 1 & 2 & 4 & 8 & 6\\ \end{bmatrix}$

Untuk mendapatkan solusinya, digunakan Gaussian Elimination

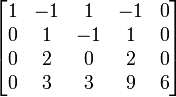$\begin{bmatrix} 1 & -1 & 1 & -1 & 0\\ 0 & 1 & -1 & 1 & 0\\ 0 & 2 & 0 & 2 & 0\\ 0 & 3 & 3 & 9 & 6\\ \end{bmatrix}$ Baris ke-2, ke-3, dan ke-4 dikurangi baris pertama

$\begin{bmatrix} 1 & -1 & 1 & -1 & 0\\ 0 & 1 & -1 & 1 & 0\\ 0 & 1 & 0 & 1 & 0\\ 0 & 1 & 1 & 3 & 2\\ \end{bmatrix}$ Baris ke-3 dibagi dengan 2, sedangkan baris ke-4 dibagi dengan 3

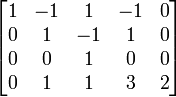$\begin{bmatrix} 1 & -1 & 1 & -1 & 0\\ 0 & 1 & -1 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 1 & 1 & 3 & 2\\ \end{bmatrix}$ Baris ke-3 dikurangi baris ke-2

$\begin{bmatrix} 1 & -1 & 1 & -1 & 0\\ 0 & 1 & -1 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 2 & 2 & 2\\ \end{bmatrix}$ Baris ke-4 dikurangi baris ke-2

$\begin{bmatrix} 1 & -1 & 1 & -1 & 0\\ 0 & 1 & -1 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 1 & 1\\ \end{bmatrix}$ Baris ke-4 dibagi dengan 2

$\begin{bmatrix} 1 & -1 & 1 & -1 & 0\\ 0 & 1 & -1 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 1\\ \end{bmatrix}$ Baris ke-4 dikurangi baris ke-3

Didapatkan persamaan linier dari persamaan matrix di atas

$\begin{matrix} a_0&+&a_1&+&a_2&+&a_3 &=&0\Longleftrightarrow a_0 = 0\\ & &a_1&-&a_2&+&a_3&=&0\Longleftrightarrow a_1 = -1\\ & & & &a_2& & &=&0\\ & & & & & &a_3&=&1\\ \end{matrix}$

Jadi, interpolasinya adalah 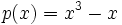$p(x) = x^3 - x\,$

Komunitas SekolahRumah Pelangi Matematika

Sabtu, 06 September 2008

Interpolasi Polinomial

Tidak ada komentar:

Mengenai Saya

Selamat Belajar dari Kak Dharma

Arsip Blog